Autor:  Miroslav Bárta, Astronomický ústav AV ČR, v.v.i., observatoř Ondřejov
Publikováno:  30. 12. 2013 - ČÁST 1.
Zdroj: psáno pro Hvězdárnu Valašské Meziříčí v rámci projektu Se Sluncem společně, prosinec 2013, pro server www.pozorovanislunce.eu

ČÁST 1. - Sluneční radioastronomie v éře ALMA - úvod a emisní mechanismy

ČÁST 2. - “Klasická” radioastronomická pozorování Slunce

ČÁST 3. - Přístroje moderní radioastronomie - ALMA

ČÁST 4. - Přístroje moderní radioastronomie

Úvod

Jako radiové vlny (v obecnějším kontextu včetně mikrovln a submilimetrových neboli terahertzových vln) obvykle označujeme výsek spektra elektromagnetického záření o vlnových délkách větších než 100μm. Tak jako i záření v jiných oblastech spektra nesou v sobě radiové vlny stopy prostředí, ve kterém vznikly nebo jím prošly, případně se od něj odrazily a otisky fyzikálních procesů v těchto prostředí probíhajících. Proto lze radiové záření použít pro vzdálenou diagnostiku parametrů látky (a její dynamiky a interakcí) na objektech blízkého i vzdáleného Vesmíru. Toho využívá vědní disciplína zvaná radioastronomie.

Historie radioastronomie začíná již rokem 1894, kdy Sir Oliver Lodge ze zákonů, kterými se řídí záření absolutně černého tělesa, odvodil myšlenku, že by šly pozorovat takovéto „dlouhé“ vlny ve slunečním záření. Bohužel, jeho pokusy tuto teorii potvrdit byly tehdy neúspěšné. Další historický milník tohoto vědního oboru přichází až v roce 1931, kdy americký inženýr Karl Jansky (jeho otec byl českého původu), který pracoval pro Bellovy telefonní laboratoře, měl za úkol vypátrat příčinu radiového šumu na přijímačích. Se svojí improvizovanou anténní soustavou (Obrázek 1) zjistil, že radiové vysílání je rušeno třemi hlavními zdroji: Lokálními blesky, vzdálenými blesky, a jakýmsi neznámým zdrojem mimo naši atmosféru. Později se ukázalo, že jde o střed Galaxie. Svoji práci sice publikoval, ale reakce na jeho objev přišla až v roce 1937. Tehdy byl muž jménem Grote Reber (radioinženýr) obeznámen s Janského prací a sám si na své zahradě postavil parabolickou anténu o průměru 9,5 metrů. V roce 1943 studoval rozložení rádiového záření po obloze na vlnové délce 187 cm a nezávisle objevil též rádiové záření Slunce o stejné vlnové délce. Před tím už radiofyzik Southworth roku 1942 pozoroval Slunce na vlnových délkách 3 cm a 10 cm a ve stejném roce byly pozorovány radiové emise Slunce Angličanem Heyem na základě hlášení radarových vojenských posádek o rušivých šumech. Práce obou badatelů však spadaly do vojenského tajemství a byly utajeny až do konce 2. světové války. Tyto objevy můžeme pokládat za zrod radiových pozorování Slunce neboli sluneční radioastronomie jakožto specifické subdisciplíny.

Velkou výhodou radioastronomie je fakt, že větší část radiového záření z Vesmíru od zhruba 10 MHz až po oblast milimetrových a submilimetrových vln prochází zemskou atmosférou (i když v případě extrémně krátkých vln pouze částečně) a pozorování v této oblasti jsou tedy dostupná z povrchu zemského bez nutnosti využívat velmi drahé kosmické technologie. Vedle oblasti viditelného (optického) záření se tak jedná o naše druhé spektrální „okno” do Vesmíru. Dostupnost pozemních pozorování umožňuje vybudování rozsáhlých (tj. s velkou sběrnou plochou) a tím pádem i citlivých aparatur. Krom toho, některé specifické procesy – zejména ty, které probíhají v horkém řídkém plazmatu, jsou často pozorovatelné výlučně na radiových vlnách. Radioastronomie, i ta sluneční, tak hraje klíčovou roli v současném výzkumu Vesmíru.

Radiové záření Slunce

Radiový tok, přicházející k nám ze Slunce, můžeme z hlediska jeho dynamiky rozčlenit do tří složek. Nejstálejší je radiové záření klidného Slunce. Tato komponenta je přítomna vždy a vykazuje jen drobné variace na časové škále řádově roků. Jde o ono Sirem Lodgem správně tušené tepelné záření Slunce, respektive jeho atmosféry. V případě plazmatu sluneční atmosféry mluvíme o detailním mechanismu vyzařování radiových vln jako o brzdném záření (viz níže oddíl o emisních mechanismech).

Druhá složka již vykazuje větší proměnlivost a její typická časová škála odpovídá 27 dnům, čili synodické periodě rotace Slunce. Mluvíme o tzv. pomalu proměnné složce. Ze souvislosti její typické periody s rotací Slunce lze vystopovat, že její původ je třeba hledat v aktivních oblastech, které představují „poruchu“ z ideální osové souměrnosti Slunce. Mnohé z nich přitom mohou přetrvat i více slunečních otoček – právě to je důvodem modulace celkového radiového toku s periodou synodické rotace Slunce. Důvody silnějšího radiového signálu z atmosféry nad aktivními oblastmi oproti klidné koróně jsou v zásadě dva: Uzavřené siločáry magnetického pole nad aktivní oblastí jsou schopny „uvěznit“ sluneční plazma ve svých smyčkách (jak se o tom můžeme přesvědčit i z družicových snímků v UV/EUV a SXR oboru) a zvýšená hustota plazmatu pak vede k většímu tepelnému vyzařování. Vedle toho se ovšem částečně uplatňuje i tzv. gyro-synchrotronový mechanismus vyzařování související s pohybem elektronů v magnetickém poli nad aktivní oblastí (viz níže).

Konečně třetí, nejrychleji proměnnou komponentou slunečního radiového toku jsou sluneční radiová vzplanutí. Jedná se o velmi dynamické jevy, kdy – v extrémních případech – jasová teplota může stoupnout až o 10 řádů během zlomku sekundy. Vzplanutí jsou velmi často spjata se slunečními erupcemi a koronálními výrony hmoty (CME). Z tohoto důvodu představuje jejich studium významný diagnostický prostředek ve výzkumu fyzikálních mechanismů slunečních erupcí. Obrovské jasové teploty, o mnoho řádů vyšší, než je skutečná kinetická teplota plazmatu ve zdroji radiového záření, ukazují, že velmi často jsou tyto radiové vlny produkovány nějakým typem netermálního vyzařování, jehož prototyp zvaný plazmová emise stručně rozebereme – vedle již zmíněného brzdného a gyro-synchrotronového záření – v následujícím oddíle.

Proč Sluníčko září na radiovlnách aneb o emisních mechanismech

Z hlediska obecné termodynamiky je zřejmé, že Slunce jako objekt s konečnou teplotou musí vyzařovat. Jakými detailními fyzikálními mechanismy se to děje v případě plazmatu sluneční atmosféry na radiových vlnách popíšeme stručně nyní. V zásadě se uvažují tři hlavní typy emisních mechanismů.

Brzdné záření

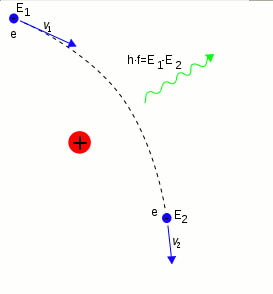
Z Maxwellovy teorie elektromagnetismu je známo, že při každém zrychleném pohybu elektrického náboje dochází k vyzařování elektromagnetických vln. V horkém prostředí sluneční koróny je látka (převážně vodík) téměř úplně v ionizovaném stavu. Elektrony, které jsou téměř 2000× lehčí než protony (natožpak jádra ostatních atomů) se tepelným neuspořádaným pohybem „proplétají“ kolem atomových jader (převážně jader vodíku, tedy protonů). Dojde-li k přiblížení elektronu ke kladně nabitému jádru, je dráha elektronu elektrostatickým přitahováním odkloněna (stává se hyperbolickou, podobně jako např. v případě přiblížení aperiodické komety ke Slunci) a elektron zakouší pohyb se zrychlením a září (Obrázek 2). Zrychlený pohyb nábojů způsobený důsledkem těchto setkání (neboli srážek) elektronů a jader v plazmatu způsobuje tedy vyzařování. Vzhledem k tomu, že ve sluneční koróně je většina srážek v důsledku malé hustoty plazmatu spíše jen vzdáleným průletem, nejsou ani zakřivení drah a jim odpovídající zrychlení příliš velká a tyto vzdálené srážky pak přispívají právě ke spíše nízkofrekvenčnímu, tedy radiovému záření. Pro úplnost poznamenejme, že v případě velkých rychlostí elektronů a hustého prostředí dochází naopak i k četným srážkám těsným – důsledkem je pak vznik krátkovlnného záření, takto např. podle našich představ vzniká tvrdé rentgenové záření (Hard X-rays/HXR) ve slunečních erupcích: je důsledkem srážek elektronů urychlených v koróně s hustou populací iontů v chromosféře, kam svazky elektronů dopadají.

Obrázek 2: Při svém pohybu kolem kladně nabitého jádra je záporně nabitý elektron přitahován k jádru elektrostatickou silou. Ta mu uděluje zrychlení, které se podle Maxwellovy teorie elektromagnetismu projeví vyzářením kvanta elektromagnetického záření.

Nicméně, kromě samotného mechanismu generace radiového záření hraje roli i otázka jeho šíření plazmatem sluneční atmosféry. V jednodušším případě, kdy se radiová vlna šíří plazmatem bez pozaďového magnetického pole, platí mezi vlnovou délkou a frekvencí tato disperzní rovnice

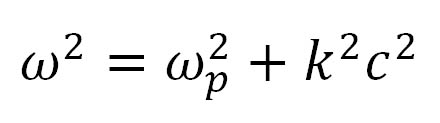
kde mezi kruhovou frekvencí ω a běžnou frekvencí f platí vztah ω=2πf a velikost vlnového vektoru k, je s obvyklejší vlnovou délkou λ spřažena relací k=2 π⁄λ. Veličina ωp se nazývá plazmová frekvence a představuje frekvenci vlastních oscilací plazmatu. Když si plazma představíme jako elektronový plyn, pohybující se mezi v podstatě stacionárními (protože o hodně těžšími) ionty, pak výchylka elektronové „tekutiny“ oproti iontové „mříži“ vede ke vzniku nábojové nerovnováhy a tím i elektrického pole. Toto pole se snaží vrátit elektrony zpět do rovnovážné polohy. Protože elektrony mají také nějakou (byť malou) hmotnost, překmitnou rovnovážnou polohu, podobně jako vychýlené závaží na pružině. Elektrické pole, mířící nyní opačným směrem, se je opět snaží vrátit do rovnovážné polohy a celý děj se opakuje – dostáváme kmity elektronové tekutiny vůči iontům právě na plazmové frekvenci.

Pro frekvenci vlastních kmitů závaží na pružině platí známý vztah

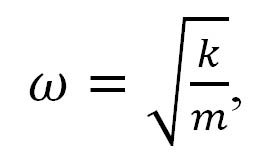
kde k je tuhost pružiny a m hmotnost závaží. V případě kmitů plazmatu plyne z Coulombova zákona elektrostatiky, že přitažlivá síla, tedy „tuhost pružiny“ by měla být úměrná součinu nábojů tedy (n_e⋅e)⋅(Z⋅n_i⋅e), kde n_e a n_i jsou částicové hustoty elektronů a iontů (tj. počet částic v jednotce objemu). Pro plně ionizované vodíkové plazma, s nímž se setkáváme ve sluneční koróně, je protonové číslo Z=1 a n_i=n_e=n, „tuhost pružiny“ tedy bude úměrná n²e². Naopak, hmotnost objemové jednotky elektronové tekutiny je úměrná n⋅m, kde m je nyní hmotnost elektronu. Z analogie s pružinovým oscilátorem tedy očekáváme, že frekvence vlastních kmitů plazmatu neboli plazmová frekvence bude úměrná odmocnině z výrazu (n²e²)/(nm)=(ne²)/m. Skutečně, podrobnější odvození dává pro plazmovou frekvenci vztah

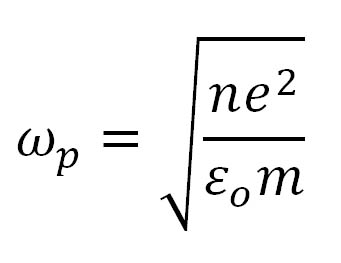
kde ε_o je permitivita vakua a do výrazu se dostala díky použité soustavě jednotek (SI).

Podstatným faktem je, že plazmová frekvence je úměrná odmocnině z elektronové hustoty (a tím pádem i materiálové hustoty plazmatu), ostatní symboly ve výrazu pro ω_p jsou konstanty. Z disperzní rovnice je patrné, že existuje minimální frekvence vln, které se mohou šířit plazmatem – je to právě ona plazmová frekvence. Podrobnějším rozborem disperzní relace, zejména výpočtem grupové rychlosti, což je rychlost jakou se šíří energie přenášená vlnou, bychom navíc zjistili, že balíky vln s frekvencí blížící se shora této limitní hodnotě f_p=ω_p /2π se plazmatem šíří velmi pomalu. Díky tomu mají dost času na to, aby díky emisnímu mechanismu získaly větší energii. Důležitým důsledkem pro chápání sluneční radioastronomie pak je to, že záření o frekvenci f k nám přichází převážně z tenké vrstvy plazmatu, jehož elektronová hustota n je taková, že jí odpovídající plazmová frekvence je velmi blízká a jen mírně nižší než frekvence pozorovaného záření. Jinými slovy, objem plazmatu s elektronovou hustotou n vyzařuje především záření o jí odpovídající plazmové frekvenci f_p. Vzhledem k tomu, že hustota plazmatu – a tedy i elektronová hustota, která je s ní pro vodíkové plně ionizované plazma sluneční koróny svázána vztahem ρ=n⋅M_H, kde M_H je hmotnost atomu vodíku – klesá (v průměru) s výškou nad sluneční fotosférou, přichází k nám krátké vlny (tedy s větší frekvencí) z větších hloubek sluneční atmosféry, kde n a tím pádem f_p je vysoké, zatímco dlouhé vlny mají původ v řidších oblastech vnější koróny. Konkrétně, dekametrové vlny mají svůj původ ve slunečním větru, metrové vlny v koróně, decimetrové zejména v hustším plazmatu aktivních oblastí v dolní koróně, centimetrové v chromosféře, případně chromosférickém materiálu „vyzdviženém“ do koróny jako jsou filamenty a protuberance, a milimetrové a submilimetrové záření přichází z fotosféry. Právě uvedené tvrzení demonstruje Obrázek 3.

Obrázek 3: Radiové mapy Slunce pro různé frekvence. Krátké vlnové délky přicházejí ze spodní chromosféry a nejvíce připomínají nám dobře známý obraz Slunce z optických pozorování. Nejdelší vlny na tomto komponovaném snímku (na frekvenci 327 MHz) k nám přicházejí z koróny, proto je obraz Slunce difúzní a výrazně větší, než samotný sluneční disk.

Tato představa platí celkem obecně, nejen pro tepelné (brzdné) záření a poskytuje základní vhled do principů sluneční radioastronomie. Samozřejmě, nelze ji brát absolutně: např. protuberance lze pozorovat i na milimetrových a submilimetrových vlnách, nejen v jejich „domovském“ centimetrovém pásmu. Pozorování na těchto vlnových délkách bude ovšem podstatně méně intenzivní než na frekvencích bližších lokální plazmové frekvenci chromosférického materiálu. Rychle se pohybující balíky submilimetrových vln (jejich grupová rychlost v protuberančním plazmatu se blíží rychlosti světla ve vakuu) nestačí při svém průletu protuberancí nastřádat potřebné množství energie. To se pak na pozorováních projeví nízkou jasovou teplotou (v radioastronomii často používaný ekvivalent pro intenzitu záření), mnohem nižší než je skutečná teplota plazmatu ve zdroji. Mluvíme pak o opticky tenké emisi, zachytit ji můžeme jen patřičně citlivými přístroji. I přes toto upřesnění ale poskytuje základní představa o frekvenci emitovaného záření klesající s výškou ve sluneční atmosféře dobré první přiblížení k porozumění sluneční radioastronomii.

Gyrosynchrotronové záření

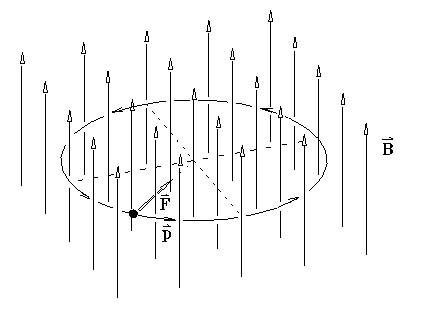
Dalším mechanismem, který se uplatňuje ve sluneční radioastronomii, je gyrosynchrotronová emise. Zrychlený pohyb nábojů, vyžadovaný Maxwellovou teorií pro generaci elektromagnetických vln je v tomto případě realizován pohybem elektronů v magnetickém poli. Magnetické pole, díky Lorentzově síle F_L=v×B nutí elektrony pohybovat se po „spirálách“ (správně šroubovicích – viz Obrázek 4) a tento křivočarý pohyb je spojen se zrychlením (způsobeným právě Lorentzovou silou). Analýzou tohoto pohybu dojdeme k závěru, že gyrosynchrotronové záření je generováno na Larmorově (též cyklotronové) frekvenci

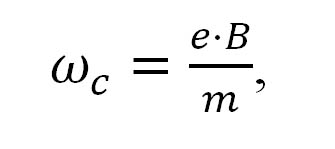
která odpovídá právě periodě elektronů při jejich cyklickém pohybu po šroubovicových trajektoriích, a na jejích násobcích – tzv. vyšších harmonických, které jsou způsobeny efektem konečného průměru šroubovice (resp. válcové plochy, po níž se vine), jinými slovy jeho nezanedbatelným rozměrem vzhledem k vlnové délce emitovaného záření. Pokud je pohyb elektronu relativistický (při vysokých teplotách), dochází navíc k rozšiřování těchto emisních „čar“ vlivem Dopplerova efektu. Pro ultra-relativistické elektrony se pak celé spektrum vyzařovaných vlnových délek slije do spojitého rozdělení, mluvíme pak o synchrotronovém záření. Vzhledem k řídkému výskytu ultra-relativistických částic na Slunci se tento extrémní případ ovšem pozoruje spíše u jiných astrofyzikálních radiových zdrojů např. u pulsarů a zbytků supernov.

Obrázek 4: Lorentzova síla nutí nabitou částici v homogenním magnetickém poli, aby se pohybovala po kruhové nebo obecně po šroubovicové dráze. Dostředivé zrychlení, udělované částici Lorentzovou silou je příčinou elektromagnetického záření.

Plazmová emise

Jiným – poněkud specifickým právě pro Slunce (i když se uvažuje i pro generaci radiovln v magnetosféře Jupitera a dalších planet a ve slunečním větru) – mechanismem radiového vyzařování je plazmová emise. Uplatňuje se především v radiových vzplanutích během slunečních erupcí. Na rozdíl od předchozích dvou mechanismů, u kterých se jedná převážně o záření způsobené zrychleným pohybem tepelných elektronů (i když ve výjimečných případech může jít i o brzdné nebo synchrotronové záření nadtepelných energetických částic), plazmová emise je typickým příkladem netermálního emisního mechanismu.

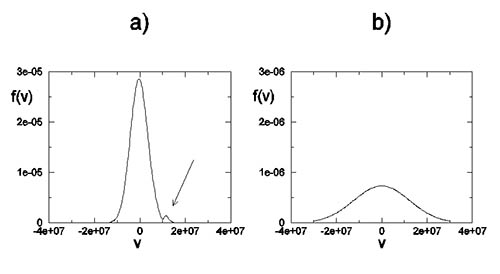
Mechanismus plazmové emise je nedílně spojen se svazky urychlených částic (elektronů) a probíhá ve dvou stupních. V první fázi svazek elektronů – urychlených nejpravděpodobněji v některé z mnoha disipativních oblastí v rekonexi magnetického pole ve sluneční erupci – vygeneruje elektrostatickou plazmovou vlnu (též Langmuirovy vlny nebo vlny Böhmovy-Grossovy). Generaci vln svazkem si můžeme představit v analogii s vytvořením rázové vlny u letadla, které překročilo rychlost zvuku, případně – asi všem bližším příkladem – může být příďová vlna tvořící se za rychle plujícím člunem. Stejným typem generace vln je i Čerenkovovo záření známé z jaderné a částicové fyziky: objevuje se u rychlých částic pohybujících se v prostředí s indexem lomu větším než jedna. Všechny uvedené případy mají společné to, že zdroj, který vlny vytváří, se pohybuje rychleji, než je rychlost šíření generovaných vln v daném prostředí. Poznamenejme, že detailní rozbor na základě kinetické teorie plazmatu nabízí na tentýž jev trochu jiný pohled: z hlediska kinetické teorie se v případě svazku pohybujícího se plazmatem jedná o nestabilní rozdělovací funkci rychlostí elektronů – v „běžném“ stavu termodynamické rovnováhy (bez přítomnosti svazků) počet elektronů o určité energii s rostoucí energií (tj. rychlostí) monotónně klesá (Boltzmanův zákon), v případě přítomnosti svazku ovšem v určité oblasti energií roste (Obrázek 5). Podobně jako v případě laseru pak mluvíme o inverzní populaci hladin. Na tomto místě je vhodné zmínit, že existuje více typů nestabilních distribučních funkcí – v případě svazků mluvíme o dvousvazkové nebo přesněji bump-on-tail nestabilitě, pokud je z nějakého důvodu větší průměrná kinetická energie pohybu elektronů kolmo k magnetickému poli než podél něj (teplotní anizotropie), může se rozvinout double-resonance nestabilita atd. Zde prezentovaný výklad plazmové emise, chápaný často úzce jako radiové záření v důsledku svazkové nestability, tak lze zobecnit i na jiné emisní mechanismy z téže třídy – základem je vždy nestabilní distribuční funkce elektronů.

Obrázek 5: Příklad nestabilní rozdělovací (neboli distribuční) funkce pro rychlosti částic v plazmatu. Pokud se plazmatem podél magnetického pole šíří svazek rychlých elektronů, projeví se to na distribuční funkci "hrbem" - ukazuje na něj šipka na panelu (a). V úzké oblasti rychlostí těsně nad 1,0 × 10⁷ m/s distribuční funkce roste s rychlostí a tedy i s energií částic (inverzní populace hladin) a není ve stavu termodynamické rovnováhy. Systém se přebytečné energie zbaví vyzářením elektrostatických plazmových vln. Zdrojem nestability ale může být i rozdílná teplota (ta je daná šířkou distribuční funkce) ve směru podél a napříč mag. pole, jak ukazuje panel (b).

Ať se již na věc díváme kterýmkoli úhlem pohledu, šířením svazku vznikají elektrostatické plazmové vlny. Jde nám o již známé plazmové oscilace popsané výše, které se v důsledku tepelných rychlostí elektronů šíří z místa svého vzniku plazmatem. Vektor intenzity elektrického pole spojeného s lokální nábojovou nerovnováhou vzniklou v důsledku posuvu elektronové tekutiny vůči iontům míří ve směru šíření těchto vln a ve stejném směru se odehrávají i kmitavé pohyby elektronů kolem své rovnovážné polohy. Oscilující magnetické pole spojené s vlnou není v takové konfiguraci v souladu s Maxwellovými rovnicemi generováno – proto mluvíme o elektrostatických vlnách. Tyto vlny jsou ovšem vázány na plazma, jímž se šíří a v žádném případě nemohou doputovat až k Zemi a být zde detekovány – podobně jako běžná zvuková vlna nemůže opustit zemskou atmosféru. Nicméně, kmitavý pohyb elektronů v těchto oscilacích je také zrychleným pohybem nábojů a podle Maxwellovy teorie by měl vést ke generaci elektromagnetických, tedy radiových vln, které se meziplanetárním prostředím už šířit mohou. To se skutečně také děje, ovšem podrobný výpočet ukáže, že příspěvky od jednotlivých elektronů se v případě elektrostatické vlny šířící se na homogenním pozadí vzájemnou interferencí úplně vyruší!

Toto ovšem neplatí, pokud se vlna šíří na pozadí s proměnlivou elektronovou hustotou. Prostorové variace elektronové hustoty mohou být způsobeny strukturováním plazmatu z vnějších příčin – např. gravitační stratifikace, přítomnost nehomogenních magnetických polí. V těchto případech je ovšem prostorová škála, na níž se elektronová hustota mění příliš veliká ve srovnání s vlnovou délkou elektrostatické vlny a interferencí tak dochází k podstatným, byť ne úplným vzájemným kompenzacím elektromagnetických příspěvků od jednotlivých elektronů. Mnohem příznivější situace nastává, pokud nehomogenita v elektronové hustotě je způsobena jinou vlnou šířící se stejným prostředím jako naše studovaná elektrostatická plazmová vlna. Takovou vlnou může být např. zvuková vlna, jev podobný zvukovým vlnám v klasickém neionizovaném plynu, nebo jiná elektrostatická plazmová vlna. Protože charakteristické prostorové škály hustotních variací jsou v těchto případech srovnatelné s vlnovou délkou, pak pro jistou elektromagnetickou vlnu, jejíž frekvence a vlnový vektor splňují rezonanční podmínku, je skládání příspěvků od jednotlivých elektronů pozitivní a interferencí tak vznikne nezanedbatelné elektromagnetické záření. Tento rozptyl elektrostatické vlny na jiné vlně (případně na jinak vzniklé hustotní nehomogenitě) představuje právě onen druhý stupeň plazmové emise. Při rozptylu na zvukové vlně (nebo statické hustotní variaci) vzniká radiové záření o frekvenci o něco málo větší než plazmová frekvence fp, při vzájemném rozptylu dvou elektrostatických vln (každá z nich má frekvenci typicky ≈fp) pak dochází k emisi radiového záření na druhé harmonické,tedy ≈2fp. Pro zájemce poznamenejme, že zvukové nebo sekundární elektrostatické vlny, na nichž se elektrostatická vlna rozptyluje, v plazmatu celkem snadno vznikají z elektrostatických vln generovaných svazkem pomocí mechanismů parametrické a modulační nestability – tyto jevy se vyskytují i ve fyzice pevných látek a technicky jsou využívány v mezifrekvenčních zesilovačích.

Přestože je mechanismus plazmové emise dvoustupňový, díky rezonančním procesům, které jsou v něm zahrnuty, je v podmínkách sluneční erupční koróny překvapivě vysoce efektivní – například v radiových vzplanutích typu decimetric spikes činí odhadovaná jasová teplota až 10¹⁵K, tedy o osm řádů více, než je odhadovaná teplota plazmatu v disipující proudové vrstvě ve sluneční erupci.

Další uvažované emisní mechanismy

Kromě uvedených tří základních mechanismů generace radiového záření ve sluneční atmosféře se zvažují i další fyzikální procesy, které by mohly vysvětlit některá pekuliární radiová pozorování. V řídké a strukturované sluneční koróně by se mohlo uplatnit tzv. přechodové záření (transition radiation). Jde o přímé vyzařování rychlých elektronů pohybujících se nehomogenním prostředím. Jeho podstata je následující: Každý náboj v plazmatu k sobě přirozeně přitahuje náboje opačného znaménka. Vzniklý „oblak“ opačných nábojů kolem nabité částice se nazývá Debyeovo stínění. Charakteristiky tohoto „oblaku“ (hustota, typická velikost) ovšem závisejí na parametrech okolního prostředí (elektronová hustota, teplota). Pohybuje-li se elektron nehomogenním prostředím, tento stínící oblak „dýchá“ a právě jeho proměnlivost je zdrojem elektromagnetického záření. K efektivnímu vyzařování je opět třeba nehomogenit s velmi krátkou prostorovou škálou.

Jinými typy emise, zajímavými zejména v souvislosti s projektem ALMA, jsou vibrační a rotační molekulové přechody, známé spíše z chladnějších končin Vesmíru (v oblasti teplotního minima sluneční atmosféry mohou – byť řídce – také některé jednodušší molekuly, např. CO, existovat) a přechody elektronů v atomu vodíku mezi velmi vysokými hladinami (tzv. rekombinační čáry). Tento typ emise představuje standardní kvantové přechody (známé z optické oblasti spektra) mezi dvěma energetickými stavy atomu nebo molekuly, kdy vyzářený foton má v souladu s Planckovou kvantovací podmínkou frekvenci

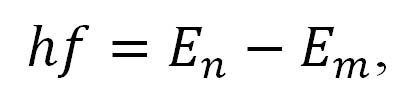
kde h je Planckova konstanta. V případě výše zmíněných přechodů padá frekvence emitovaného záření do oblasti milimetrových a submilimetrových vln, na něž se ALMA specializuje.
 

Pokračování článku Část 2. - “Klasická” radioastronomická pozorování Slunce